Source: David R. Goff. Fiber Optic Video Transmission, 1st ed. Focal Press: Woburn, Massachusetts, 2003

and other private writings.

Technology Basics

Forward Error Correction (FEC) is a technique that has been used for a number of years in submarine fiber optic systems. It is a technique that allows for near perfect data transmission accuracy even when faced with a noisy transmission channel. A number of FEC algorithms are being used including Hamming code, Reed-Solomon code and Bose-Chandhuri-Hocquenghem code.

By way of example, consider the operation of your cell phone when you’re about to have your signal fade away. Let’s say you wanted to tell the person on the other end of the call a sequence of numbers. There are several techniques that could be used to improve accuracy; For instance, assume the list of numbers that you wish to transmit might be 7, 3, 8, 10, 12, and 21. One method would be to repeat the list of numbers two times and have the person at the receive end write down each list and compare them, If they match, the data transmission is probably OK. The drawback is that, since you have to send all data two times, the throughput of the system is cut in half and if the lists don’t match, you will have no idea which one is correct. Using this most basic method, to ensure that you could verify good transmission and correct some errors, you’d have to send the list three times and verify that two out of the three transmissions matched for each number. A second method might be to first announce that you will be sending six numbers, then send the six numbers followed by the total of the six numbers. The transmission sequence would then be 6, 7, 3, 8, 10, 12, 21, and 61. The person at the receive end would look at the first number and then ensure that the correct number of additional numbers is received and then verify that the number at the end of the sequence that is the sum of the transmitted numbers. This method only requires less additional data to be sent. If any number is received wrong or missed, then the check sum number at the end of the transmission will not match the sum of the transmitted numbers. The methods shown are good examples of error detecting codes. They allow you to determine if the transmission was accurate, but they don’t allow you to correct the errors. Note: The term "Forward" in FEC implies that the error correction is accomplished by some information that is sent along with the data transmission.
 

Error correcting codes are considerable more complex than error detecting codes and are ubiquitous in nearly every modern communication application. Error correcting codes even find widespread use in CD and DVD players. In order to present an example of an error correcting code, we need to introduce and define two terms; binary and parity. In the prior examples of error detecting codes, we used numbers like 7, 3, 8, etc. These are base ten numbers, the counting systems familiar to us in everyday life. Binary numbers are base two numbers. They can only have two possible values, 0 or 1. Binary is the system used in nearly all communication and computer systems. The second concept that we need to understand, is a concept called parity. Parity is a term that is used in binary communication systems to indicate whether the numbers of 1's in a transmission is even or odd. If the number of 1's is an even number, then parity is said to be even and conversely for odd parity.

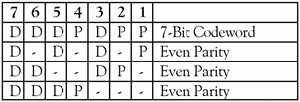
The Hamming Code

Consider a message having four data bits (D) which is to be transmitted as a 7-bit codeword by adding three error control bits. This would be called a (7, 4) code. That means that the total codeword length is seven bits, but only four of those bits are actually data. The three bits to be added are three EVEN Parity bits (P), where the parity of each is computed on different subsets of the message bits as shown in Figure 1.

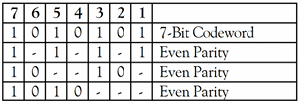
For example, the message 1011 would be sent as 1010101 as demonstrated in Figure 2.

Figure 1 - EVEN Parity Algorithm

Figure 2 - Sample Message Computation

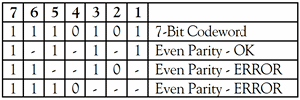
It may now be observed that if an error occurs in any of the seven bits, that error will affect different combinations of the three parity bits depending on the bit position.

For example, suppose the above message 1010101 is sent and a single bit error occurs such that the codeword 1110101 is received:

Transmitted                     Received

Message                         Message
1 0 1 0 1 0 1 -----------> 1 1 1 0 1 0 1
 

The above error can be corrected by examining which of the three parity bits was affected by the bad bit as shown in Figure 3.

The pattern of the parity bit errors indicates which bit in the codeword is in error, thus it can be corrected.

Figure 3 - Return to Zero (RZ) Format

The value of the Hamming code can be summarized:

1. Detection of 2-bit errors (assuming no correction is attempted)

2. Correction of single bit errors

3. Cost of 3 bits added to a 4-bit message

The ability to correct single bit errors comes at a cost which is less than sending the entire message twice. (Recall that simply sending a message twice accomplishes no error correction.) As the size of the codeword becomes very large, the extra burden of the error correcting bits becomes negligible. For instance, one possible Hamming code considered for fiber optic submarine transmission is the (18880, 18865) code. That means that the 18,880 bit codeword contains 18,865 actual data bits and 15 error correction bits. More robust forms of FEC may include many more error correction bits so that multiple bit errors can be detected and corrected in each codeword.

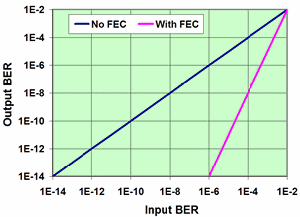
FEC on fiber optics uses a method similar to the Hamming code error correction given above. Typically, for an OC-192 system, there is roughly a 7% overhead added by the FEC process. The base data rate of 10 Gb/s is increased to about 10.7 Gb/s. So for every 1,000 bits of data transmitted, an additional 70 bits of FEC are sent along to allow verification of the integrity of the received data and to correct many of the errors that can occur during transmission over the optical fiber. Figure 4 shows the effect of FEC on the system BER (Bit error Rate). BER is a measure of what fraction of the received bits have errors. A BER of 10-3 means that one out of every 1,000 bits is incorrect. The solid curve shows the result if a given system does not have FEC. The input BER is a measure of errors that occur in the transmission channel. Since, the system lacks FEC, any errors that occur during transmission appear at the system output. The dotted line shows what might happen if an FEC is added to the system. Whereas before an input BER of 10^-6 would yield an output BER of 10^-6, with FEC it now yields an output BER of 10^-14, a very substantial improvement.

Adding FEC to the system allows the designer to push distances and data rates farther than might be possible with any other technique or it would allow a system to have more operating margin.

Figure 4 - Impact of FEC